background
The AVL tree is a balanced binary search tree. In 1962, GM Adelson-Velsky and EM Landis published in their paper "An algorithm for the organization of information."
The so-called balance means that the height difference between the left and right subtrees under any node in the tree does not exceed one. (The height convention of the tree for this article is: the height of the empty node is 0, and the height of the leaf node is 1.)
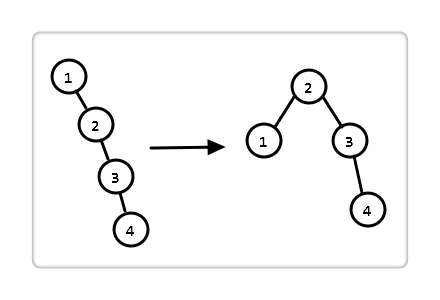
What is the difference between the AVL tree and the ordinary binary search tree? As shown in the figure, if we insert a set of ordered ascending or descending data, an ordinary binary search tree will inevitably degenerate into a single linked list, and its search efficiency will be reduced to O(n). The AVL tree can always maintain O(logn) time complexity due to its balance.
Concrete implementation and code analysis
After we have finished inserting or deleting, it is likely to cause a node to lose balance, then we need to rotate the unbalanced node to restore its balance.
After analysis, whether it is insert or delete, they will have four imbalances: left and left imbalance, right and left imbalance, left and right imbalance, right and left imbalance. Therefore, each time we encounter an imbalance, we only need to judge which imbalance is, and then carry out the corresponding recovery and balance operation.
Well, let's take the insertion operation as an example to see the four unbalanced mountains. (The following unified convention: the red node is the newly inserted node, and the y node is the unbalanced node)
(1) Left and left imbalance
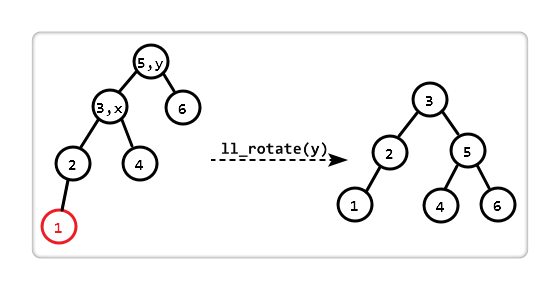
The so-called left-left, that is, the left subtree of the "unbalanced node" is 2 higher than the right subtree, and the left subtree under the left child is 1 higher than the right subtree.
We only need to "left-left rotation (ll_rotate)" on the "subtree with y as the root". After one rotation, balance is restored.
Node * AVL::ll_rotate(Node * y)
{
Node * x = y->left;
Y->left = x->right;
X->right = y;
Y->height = max(get_height(y->left), get_height(y->right)) + 1;
X->height = max(get_height(x->left), get_height(x->right)) + 1;
Return x;
}
(2) Right and right imbalance
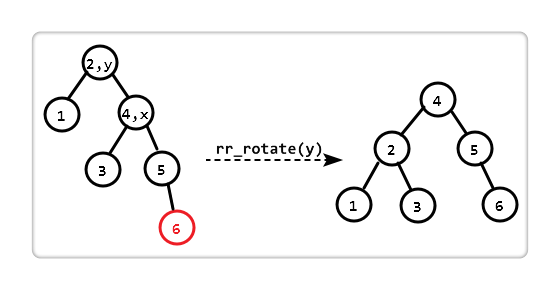
The so-called right and right, that is, the right subtree of the "unbalanced node" is 2 higher than the left subtree, and the right subtree under the right child is 1 higher than the left subtree.
We only need to "right-rotate (rr_rotate)" to the "subtree with y as the root". After one rotation, balance is restored.
Node * AVL::rr_rotate(Node * y)
{
Node * x = y->right;
Y->right = x->left;
X->left = y;
Y->height = max(get_height(y->left), get_height(y->right)) + 1;
X->height = max(get_height(x->left), get_height(x->right)) + 1;
Return x;
}
(3) imbalance around
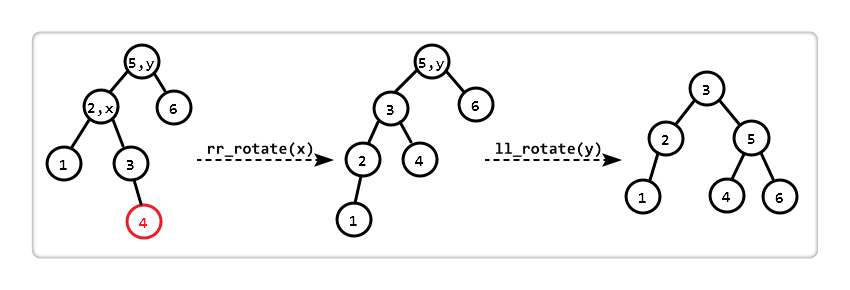
The so-called left and right, that is, the "unbalanced node" of the left subtree is 2 higher than the right subtree, and the right subtree under the left child is 1 higher than the left subtree.
Observe that if you first perform a "right-right rotation (rr_rotate)" on the "sub-tree with x as the root", then the "sub-tree with y as the root" just coincides with the "left-left imbalance", so "left again" Rotate left (ll_rotate)". After two rotations, the balance is restored.
Node * AVL::lr_rotate(Node * y)
{
Node * x = y->left;
Y->left = rr_rotate(x);
Return ll_rotate(y);
}
(4) Right and left imbalance
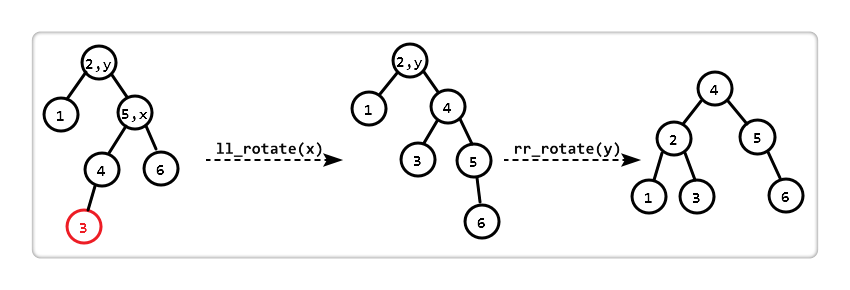
The so-called right-left, that is, the right subtree of the "unbalanced node" is 2 higher than the left subtree, and the left subtree under the right child is 1 higher than the right subtree.
Observed that if "left-left rotation (ll_rotate)" is performed on "sub-tree with x as root", then "sub-tree with y as root" just coincides with "right-right imbalance", so "right again" Rotate right (rr_rotate)". After two rotations, the balance is restored.
Node * AVL::rl_rotate(Node * y)
{
Node * x = y->right;
Y->right = ll_rotate(x);
Return rr_rotate(y);
}
Insert operation
After the successful insertion, in the recursive backtracking, the passed nodes are judged to be unbalanced in turn. If the imbalance is needed, the corresponding rotation operation is needed to restore the balance. During this period, the root node originally used as a subtree will be The rotation is replaced, so setting insert_real( ) returns the new root node so that the root node can be updated in real time.
The insert operation implementation code is as follows:
Int AVL::get_height(Node * node)
{
If (node ​​== nullptr)
Return 0;
Return node->height;
}
Int AVL::get_balance(Node * node)
{
If (node ​​== nullptr)
Return 0;
Return get_height(node->left) - get_height(node->right);
}
Node * AVL::insert_real(int key, Node * node)
{
If (node ​​== nullptr)
Return new Node(key);
If (key < node->key)
Node->left = insert_real(key, node->left);
Else if (key > node->key)
Node->right = insert_real(key, node->right);
Else
Return node;
Node->height = max(get_height(node->left), get_height(node->right)) + 1;
Int balance = get_balance(node);
// Left and left imbalance
If (balance > 1 && get_balance(node->left) > 0)
Return ll_rotate(node);
// Right and right imbalance
If (balance < -1 && get_balance(node->right) < 0)
Return rr_rotate(node);
// left and right imbalance
If (balance > 1 && get_balance(node->left) < 0)
Return lr_rotate(node);
// right and left imbalance
If (balance < -1 && get_balance(node->right) > 0)
Return rl_rotate(node);
Return node;
}
Void AVL::insert(int key)
{
Header->left = insert_real(key, header->left);
}
Find operation
Node * AVL::find_real(int key, Node * node)
{
If (node ​​== nullptr)
Return nullptr;
If (key < node->key)
Return find_real(key, node->left);
Else if (key > node->key)
Return find_real(key, node->right);
Else
Return node;
}
Node * AVL::find(int key)
{
Return find_real(key, header->left);
}
Delete operation
The four imbalances of the delete operation are the same as the insert operation, the reader can refer to the previous article. Here is the implementation code for the delete operation:
Node * AVL::erase_real(int key, Node * node)
{
If (node ​​== nullptr)
Return node;
If (key < node->key)
Node->left = erase_real(key, node->left);
Else if (key > node->key)
Node->right = erase_real(key, node->right);
Else
{
If (node->left && node->right)
{
// find the successor node
Node * x = node->right;
While (x->left)
x = x->left;
// subsequent direct copy
Node->key = x->key;
// convert to delete successor
Node->right = erase_real(x->key, node->right);
}
Else
{
Node * t = node;
Node = node->left ? node->left : node->right;
Delete t;
If (node ​​== nullptr)
Return nullptr;
}
}
Node->height = max(get_height(node->left), get_height(node->right)) + 1;
Int balance = get_balance(node);
// Left and left imbalance
If (balance > 1 && get_balance(node->left) >= 0) // need to add an equal sign
Return ll_rotate(node);
// Right and right imbalance
If (balance < -1 && get_balance(node->right) <= 0) // need to add an equal sign
Return rr_rotate(node);
// left and right imbalance
If (balance > 1 && get_balance(node->left) < 0)
Return lr_rotate(node);
// right and left imbalance
If (balance < -1 && get_balance(node->right) > 0)
Return rl_rotate(node);
Return node;
}
Void AVL::erase(int key)
{
Header->left = erase_real(key, header->left);
}
Complete code
/**
*
* author : Liu Yi (Limer)
* date : 2017-08-17
* mode : C++
*/
#include
#include
Using namespace std;
Struct Node
{
Int key;
Int height;
Node * left;
Node * right;
Node(int key = 0)
{
This->key = key;
This->height = 1;
This->left = this->right = nullptr;
}
};
Class AVL
{
Private:
Node * header;
Private:
Node * ll_rotate(Node * y);
Node * rr_rotate(Node * y);
Node * lr_rotate(Node * y);
Node * rl_rotate(Node * y);
Void destroy(Node * node);
Int get_height(Node * node);
Int get_balance(Node * node);
Node * insert_real(int key, Node * node);
Node * find_real(int key, Node * node);
Node * erase_real(int key, Node * node);
Void in_order(Node * node);
Public:
AVL();
~AVL();
Void insert(int key);
Node * find(int key);
Void erase(int key);
Void print();
};
Node * AVL::ll_rotate(Node * y)
{
Node * x = y->left;
Y->left = x->right;
X->right = y;
Y->height = max(get_height(y->left), get_height(y->right)) + 1;
X->height = max(get_height(x->left), get_height(x->right)) + 1;
Return x;
}
Node * AVL::rr_rotate(Node * y)
{
Node * x = y->right;
Y->right = x->left;
X->left = y;
Y->height = max(get_height(y->left), get_height(y->right)) + 1;
X->height = max(get_height(x->left), get_height(x->right)) + 1;
Return x;
}
Node * AVL::lr_rotate(Node * y)
{
Node * x = y->left;
Y->left = rr_rotate(x);
Return ll_rotate(y);
}
Node * AVL::rl_rotate(Node * y)
{
Node * x = y->right;
Y->right = ll_rotate(x);
Return rr_rotate(y);
}
Void AVL::destroy(Node * node)
{
If (node ​​== nullptr)
Return;
Destroy(node->left);
Destroy(node->right);
Delete node;
}
Int AVL::get_height(Node * node)
{
If (node ​​== nullptr)
Return 0;
Return node->height;
}
Int AVL::get_balance(Node * node)
{
If (node ​​== nullptr)
Return 0;
Return get_height(node->left) - get_height(node->right);
}
Node * AVL::insert_real(int key, Node * node)
{
If (node ​​== nullptr)
Return new Node(key);
If (key < node->key)
Node->left = insert_real(key, node->left);
Else if (key > node->key)
Node->right = insert_real(key, node->right);
Else
Return node;
Node->height = max(get_height(node->left), get_height(node->right)) + 1;
Int balance = get_balance(node);
// Left and left imbalance
If (balance > 1 && get_balance(node->left) > 0)
Return ll_rotate(node);
// Right and right imbalance
If (balance < -1 && get_balance(node->right) < 0)
Return rr_rotate(node);
// left and right imbalance
If (balance > 1 && get_balance(node->left) < 0)
Return lr_rotate(node);
// right and left imbalance
If (balance < -1 && get_balance(node->right) > 0)
Return rl_rotate(node);
Return node;
}
Node * AVL::find_real(int key, Node * node)
{
If (node ​​== nullptr)
Return nullptr;
If (key < node->key)
Return find_real(key, node->left);
Else if (key > node->key)
Return find_real(key, node->right);
Else
Return node;
}
Node * AVL::erase_real(int key, Node * node)
{
If (node ​​== nullptr)
Return node;
If (key < node->key)
Node->left = erase_real(key, node->left);
Else if (key > node->key)
Node->right = erase_real(key, node->right);
Else
{
If (node->left && node->right)
{
// find the successor node
Node * x = node->right;
While (x->left)
x = x->left;
// subsequent direct copy
Node->key = x->key;
// convert to delete successor
Node->right = erase_real(x->key, node->right);
}
Else
{
Node * t = node;
Node = node->left ? node->left : node->right;
Delete t;
If (node ​​== nullptr)
Return nullptr;
}
}
Node->height = max(get_height(node->left), get_height(node->right)) + 1;
Int balance = get_balance(node);
// Left and left imbalance
If (balance > 1 && get_balance(node->left) >= 0) // need to add an equal sign
Return ll_rotate(node);
// Right and right imbalance
If (balance < -1 && get_balance(node->right) <= 0) // need to add an equal sign
Return rr_rotate(node);
// left and right imbalance
If (balance > 1 && get_balance(node->left) < 0)
Return lr_rotate(node);
// right and left imbalance
If (balance < -1 && get_balance(node->right) > 0)
Return rl_rotate(node);
Return node;
}
Void AVL::in_order(Node * node)
{
If (node ​​== nullptr)
Return;
In_order(node->left);
Cout << node->key << " ";
In_order(node->right);
}
AVL::AVL()
{
Header = new Node(0);
}
AVL::~AVL()
{
Destroy(header->left);
Delete header;
Header = nullptr;
}
Void AVL::insert(int key)
{
Header->left = insert_real(key, header->left);
}
Node * AVL::find(int key)
{
Return find_real(key, header->left);
}
Void AVL::erase(int key)
{
Header->left = erase_real(key, header->left);
}
Void AVL::print()
{
In_order(header->left);
Cout << endl;
}
Int main()
{
AVL avl;
// test "insert"
Avl.insert(7);
Avl.insert(2);
Avl.insert(1); avl.insert(1);
Avl.insert(5);
Avl.insert(3);
Avl.insert(6);
Avl.insert(4);
Avl.insert(9);
Avl.insert(8);
Avl.insert(11); avl.insert(11);
Avl.insert(10);
Avl.insert(12);
Avl.print(); // 1 2 3 4 5 6 7 8 9 10 11 12
// test "find"
Node * p = nullptr;
Cout << ((p = avl.find(2)) ? p->key : -1) << endl; // 2
Cout << ((p = avl.find(100)) ? p->key : -1) << endl; // -1
// test "erase"
Avl.erase(1);
Avl.print(); // 2 3 4 5 6 7 8 9 10 11 12
Avl.erase(9);
Avl.print(); // 2 3 4 5 6 7 8 10 11 12
Avl.erase(11);
Avl.print(); // 2 3 4 5 6 7 8 10 12
Return 0;
}
The initially constructed AVL tree is shown below:
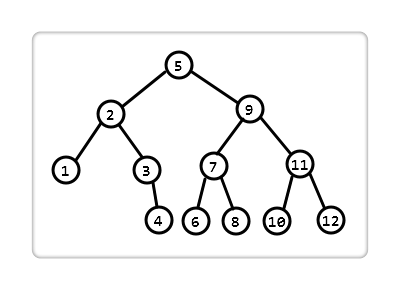
to sum up
Compared with the binary search tree, the AVL tree is characterized by more stable time complexity, but the disadvantages are also obvious.
In the insert operation, at most one recovery operation is required, and the magnitude of the recursive backtracking is O(logn). One thing that needs our attention is that after the first unbalanced node is restored, the recursive backtracking should stop immediately (because the father of the unbalanced node and his ancestors are definitely in equilibrium).
But let the "recursive backtracking" stop midway, it is not easy to achieve, so my coding program will inevitably continue to backtrack until the root node of the whole tree, and these backtracking are not necessary. (Thank you for the LLL reminder that if you add a father node to the node, you can solve the problem of recursive backtracking.)
In the deletion operation, if there is an imbalance, at least one recovery operation is required, and the magnitude of the recursive backtracking is also O(logn). Unlike the insert operation, when the first unbalanced node is restored to equilibrium, its father or its ancestors may also be unbalanced (see the figure below, delete 1), so the traceback of the delete operation is necessary.
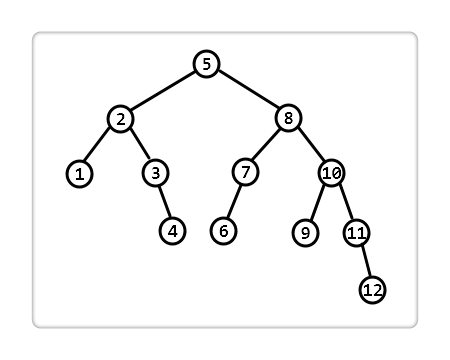
There is no point in the discussion without reference comparison, so this article ends here. Interested friends can read the article behind "Red Black Tree" and "A Comparison between AVL Tree and Red Black Tree".
ZGAR bar 600 Puffs
ZGAR electronic cigarette uses high-tech R&D, food grade disposable pod device and high-quality raw material. All package designs are Original IP. Our designer team is from Hong Kong. We have very high requirements for product quality, flavors taste and packaging design. The E-liquid is imported, materials are food grade, and assembly plant is medical-grade dust-free workshops.
Our products include disposable e-cigarettes, rechargeable e-cigarettes, rechargreable disposable vape pen, and various of flavors of cigarette cartridges. From 600puffs to 5000puffs, ZGAR bar Disposable offer high-tech R&D, E-cigarette improves battery capacity, We offer various of flavors and support customization. And printing designs can be customized. We have our own professional team and competitive quotations for any OEM or ODM works.
We supply OEM rechargeable disposable vape pen,OEM disposable electronic cigarette,ODM disposable vape pen,ODM disposable electronic cigarette,OEM/ODM vape pen e-cigarette,OEM/ODM atomizer device.

Disposable Vape, bar 600puffs, ZGAR bar disposable, Disposable E-cigarette, OEM/ODM disposable vape pen atomizer Device E-cig
ZGAR INTERNATIONAL(HK)CO., LIMITED , https://www.szdisposable-vape.com